Калькулятор с решениями примеров и уравнений онлайн и выводом графиков
Содержание:
Матрицы и определители
Пример 1. Сумма матриц
Дано:
Матрицы A и B., Найти:
Сумму матриц A + B = C.C- ?
Решение:
Для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах.
Таким образом, суммой двух матриц A и B является матрица:
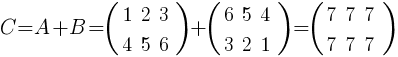
Ответ:
Пример 2. Умножение матрицы на число
Дано:
Матрица
Число k=2.
Найти:
Произведение матрицы на число: A × k = BB — ?
Решение:
Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число.
Таким образом, произведение матрицы A на число k есть новая матрица:
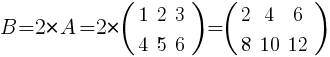
Ответ:
Пример 3. Умножение матриц
Дано:
Матрица ;
Матрица .
Найти:
Произведение матриц: A × B = CC — ?
Решение:
Каждый элемент матрицы С = A × B, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Строки матрицы А умножаем на столбцы матрицы В и получаем:

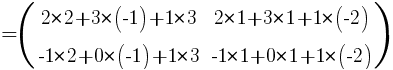
Ответ:
Пример 4. Транспонирование матрицы
Дано:
Матрица .
Найти:
Найти матрицу транспонированную данной.AT — ?
Решение:
Транспонирование матрицы А заключается в замене строк этой матрицы ее столбцами с сохранением их номеров. Полученная матрица обозначается через AT
Ответ:
Пример 5. Обратная матрица
Дано:
Матрица .
Найти:
Найти обратную матрицу для матрицы A.A-1 — ?
Решение:
Находим det A и проверяем det A ≠ 0:. det A = 5 ≠ 0.
Составляем вспомогательную матрицу AV из алгебраических дополнений Aij: .
Транспонируем матрицу AV:.
Каждый элемент, полученной матрицы, делим на на det A: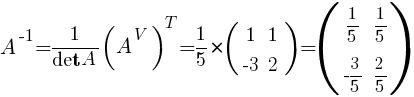
Ответ:
Пример 6. Ранг матрицы
Дано:
Матрица .
Найти:
Ранг матрицы A.r(A) — ?
Решение:
Ранг матрицы A — это число, равное максимальному порядку отличных от нуля миноров Mk этой матрицы. Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований.
Вычислим ранг матрицы, применив .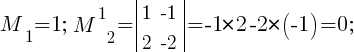
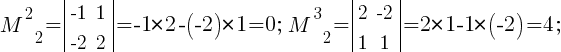
M32≠0; 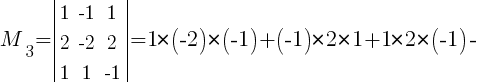
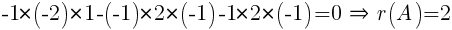 .
.
Ответ: r(A) = 2
Пример 7. Определитель квадратной матрицы
Дано:
Матрица .
Найти:
Определитель |A| матрицы A.|A| — ?
Решение:
Каждой квадратной матрице А можно поставить в соответствие число, которое называется ее определителем и обозначается det А или |А|. Определитель матрицы третьего порядка вычисляется через ее элементы, по следующей формуле:
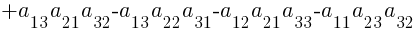
Тогда, для данной в примере матрицы A, определитель |A| будет равен: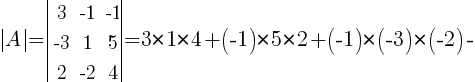
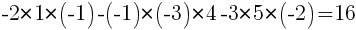
Ответ: |A| = 16.
Пример 8. Минор и алгебраическое дополнение
Дано:
Матрица .
Найти:
Минор и алгебраическое дополнение элемента a21 определителя |A| матрицы A.Δ21 — ? A21 — ?
Решение:
Запишем определитель матрицы A: .
Минор элемента a21 определителя |A|- это определитель, который получится из данного вычеркиванием 2-й строки и 1-го столбца. Для минора используют обозначение Δ21.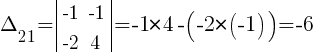
Алгебраическое дополнение A21 элемента a21 в определителе — это число, которое вычисляется по правилу: Aij = (-1)i+j · Δij, где Δij — соответствующий минор. Тогда, подставив данные в формулу, получим:A21 = (-1)2+1 · (-6) = 6.
Ответ: Δ21 = -6; A21 = 6.
Данный онлайн калькулятор может
- Корректно выполнять стандартные математические функции, записанные одной строкой типа — 12*3-(7/2) и может обрабатывать числа больше, чемсчитаем огромные числа в онлайн калькулятореМы даже не знаем, как такое число назвать правильно (тут 34 знака и это совсем не предел).
- Кроме тангенса, косинуса, синуса и других стандартных функций — калькулятор поддерживает операции по расчёту арктангенса, арккотангенса и прочих.
- Доступны в арсенале логарифмы, факториалы и другие интересные функции
- Данный онлайн калькулятор умеет строить графики!!!
Для построения графиков, сервис использует специальную кнопку (график серый нарисован) или буквенное представление этой функции (Plot). Чтобы построить график в онлайн калькуляторе, достаточно записать функцию: plot(tan(x)),x=-360..360.
Мы взяли самый простой график для тангенса, и после запятой указали диапазон переменной X от -360 до 360.
Построить можно абсолютно любую функцию, с любым количеством переменных, например такую: plot(cos(x)/3z, x=-180..360,z=4) или ещё более сложную, какую сможете придумать
Обращаем внимание на поведение переменной X — указан промежуток от и до с помощью двух точек
Единственный минус (хотя трудно назвать это минусом) этого онлайн калькулятора это то, что он не умеет строить сферы и другие объёмные фигуры — только плоскость.
Как работать с Математическим калькулятором
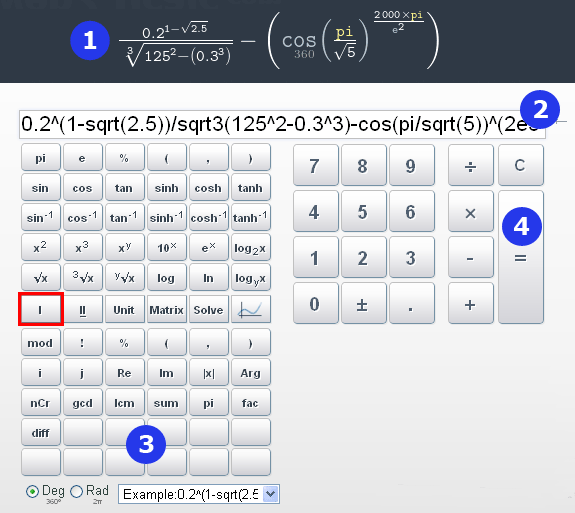
1. Дисплей (экран калькулятора) отображает введенное выражение и результат его расчёта обычными символами, как мы пишем на бумаге. Это поле предназначено просто для просмотра текущей операции. Запись отображается на дисплее по мере набора математического выражения в строке ввода.
2. Поле ввода выражения предназначено для записи выражения, которое нужно вычислить. Здесь следует отметить, что математические символы, используемые в компьютерных программах, не всегда совпадают с теми, которые обычно мы применяем на бумаге. В обзоре каждой функции калькулятора вы найдёте правильное обозначение конкретной операции и примеры расчётов в калькуляторе. На этой странице ниже приводится перечень всех возможных операций в калькуляторе, также с указанием их правильного написания.
3. Панель инструментов — это кнопки калькулятора, которые заменяют ручной ввод математических символов, обозначающих соответствующую операцию. Некоторые кнопки калькулятора (дополнительные функции, конвертер величин, решение матриц и уравнений, графики) дополняют панель задач новыми полями, где вводятся данные для конкретного расчёта. Поле «History» содержит примеры написания математических выражений, а также ваши шесть последних записей.
Обратите внимание, при нажатии кнопок вызова дополнительных функций, конвертера величин, решения матриц и уравнений, построения графиков вся панель калькулятора смещается вверх, закрывая часть дисплея. Заполните необходимые поля и нажмите клавишу «I» (на рисунке выделена красным цветом), чтобы увидеть дисплей в полный размер
4. Цифровая клавиатура содержит цифры и знаки арифметических действий. Кнопка «С» удаляет всю запись в поле ввода выражения. Чтобы удалять символы по одному, нужно использовать стрелочку справа от строки ввода.
Старайтесь всегда закрывать скобки в конце выражения. Для большинства операций это некритично, калькулятор online рассчитает всё верно. Однако, в некоторых случаях возможны ошибки. Например, при возведении в дробную степень незакрытые скобки приведут к тому, что знаменатель дроби в показателе степени уйдет в знаменатель основания. На дисплее закрывающая скобка обозначена бледно-серым цветом, её нужно закрыть, когда запись закончена.
| Клавиша | Символ | Операция |
|---|---|---|
| pi | pi | Постоянная pi |
| е | е | Число Эйлера |
| % | % | Процент |
| ( ) | ( ) | Открыть/Закрыть скобки |
| , | , | Запятая |
| sin | sin(?) | Синус угла |
| cos | cos(?) | Косинус |
| tan | tan(y) | Тангенс |
| sinh | sinh() | Гиперболический синус |
| cosh | cosh() | Гиперболический косинус |
| tanh | tanh() | Гиперболический тангенс |
| sin-1 | asin() | Обратный синус |
| cos-1 | acos() | Обратный косинус |
| tan-1 | atan() | Обратный тангенс |
| sinh-1 | asinh() | Обратный гиперболический синус |
| cosh-1 | acosh() | Обратный гиперболический косинус |
| tanh-1 | atanh() | Обратный гиперболический тангенс |
| x2 | ^2 | Возведение в квадрат |
| х3 | ^3 | Возведение в куб |
| xy | ^ | Возведение в степень |
| 10x | 10^() | Возведение в степень по основанию 10 |
| ex | exp() | Возведение в степень числа Эйлера |
| vx | sqrt(x) | Квадратный корень |
| 3vx | sqrt3(x) | Корень 3-ей степени |
| yvx | sqrt(x,y) | Извлечение корня |
| log2x | log2(x) | Двоичный логарифм |
| log | log(x) | Десятичный логарифм |
| ln | ln(x) | Натуральный логарифм |
| logyx | log(x,y) | Логарифм |
| I / II | Сворачивание/Вызов дополнительных функций | |
| Unit | Конвертер величин | |
| Matrix | Матрицы | |
| Solve | Уравнения и системы уравнений | |
| Построение графиков | ||
| Дополнительные функции (вызов клавишей II) | ||
| mod | mod | Деление с остатком |
| ! | ! | Факториал |
| i / j | i / j | Мнимая единица |
| Re | Re() | Выделение целой действительной части |
| Im | Im() | Исключение действительной части |
| |x| | abs() | Модуль числа |
| Arg | arg() | Аргумент функции |
| nCr | ncr() | Биноминальный коэффициент |
| gcd | gcd() | НОД |
| lcm | lcm() | НОК |
| sum | sum() | Суммарное значение всех решений |
| fac | factorize() | Разложение на простые множители |
| diff | diff() | Дифференцирование |
| Deg | Градусы | |
| Rad | Радианы |
Инженерный калькулятор онлайн
Спешим представить всем желающим бесплатный инженерный калькулятор. С его помощью любой учащийся может быстро и, что самое главное, легко выполнять различного рода математические вычисления онлайн.
Калькулятор взят с сайта — web 2.0 scientific calculator
Инженерному калькулятору под силу выполнить как простые арифметические действия, так и довольно сложные математические расчеты.
Web20calc — инженерный калькулятор, который имеет огромное количество функций, к примеру, как вычисление всех элементарных функций. Также калькулятор поддерживает тригонометрические функции, матрицы, логарифмы и даже построение графиков.
Несомненно, Web20calc будет интересен той группе людей, которая в поиске простых решений набирает в поисковых системах запрос: математический онлайн калькулятор. Бесплатное веб-приложение поможет сиюминутно посчитать результат какого-нибудь математического выражения, к примеру, вычесть, сложить, поделить, извлечь корень, возвести в степень и т.д.
В выражении можно воспользоваться операциями возведения в степень, сложения, вычитания, умножения, деления, процентом, константой ПИ. Для сложных вычислений следует указывать скобки.
Возможности инжинерного калькулятора:
1. основные арифметические действия;
2. работа с цифрами в стандартном виде;
3. вычисление тригонометрических корней, функций, логарифмов, возведение в степень;
4. статистические расчеты: сложение, среднее арифметическое или среднеквадратическое отклонение;
5. применение ячейки памяти и пользовательских функций 2-х переменных;
6. работа с углами в радианной и градусной мерах.

Инженерный калькулятор допускает использование разнообразных математических функций:
• извлечение корней (корень квадратный, кубический, а также корень n-ой степени);
• ex (e в x степени), экспонента;
• тригонометрические функции: синус — sin, косинус — cos, тангенс — tan;
• обратные тригонометрические функции: арксинус — sin-1, арккосинус — cos-1, арктангенс — tan-1;
• гиперболические функции: синус — sinh, косинус — cosh, тангенс — tanh;
• логарифмы: двоичный логарифм по основанию два — log2x, десятичный логарифм по основанию десять — log, натуральный логарифм – ln.
В этот инженерный калькулятор также включён калькулятор величин с возможностью конвертирования физических величин для различных систем измерений – компьютерные единицы, расстояние, вес, время и т.д. С помощью данной функции можно моментально произвести перевод миль в километры, фунтов в килограммы, секунд в часы и т.д.
Чтобы произвести математические расчеты, для начала введите последовательность математические выражения в соответствующее поле, затем нажмите на знак равенства и лицезрейте результат. Можно вводить значения прямо с клавиатуры (для этого область калькулятора должна быть активна, следовательно, нелишним будет поставить курсор в поле ввода). Помимо прочего, данные можно вносить при помощи кнопок самого калькулятора.
Для построения графиков в поле ввода следует записать функцию так, как указанно в поле с примерами или воспользуйтесь специально предназначенной для этого панелью инструментов (чтобы в нее перейти нажмите на кнопку с иконкой в виде графика). Для конвертации величин нажмите Unit, для проведения работ с матрицами – Matrix.
Системы линейных уравнений
Пример 9. Метод Крамера
Дано:
Система линейных уравнений
Найти:
Решение системы линейных уравнений методом Крамера.x1, x2, x3— ?
Составляем матрицу B из свободных членов данной системы уравнений — матрицу-столбец свободных членов:
Решаем пример методом Крамера, используя .
Условие Δ ≠ 0 выполняется, значит система совместна и определена, причём единственное решение вычисляется по формулам Крамера:
Δ1 — 1-й вспомогательный определитель системы, получается из Δ заменой 1-го столбца на столбец свободных членов:
Δ2 — 2-й вспомогательный определитель системы, получается из Δ заменой 2-го столбца на столбец свободных членов:
Δ3 — 3-й вспомогательный определитель системы, получается из Δ заменой 3-го столбца на столбец свободных членов:
Подставив полученные значения в формулы Крамера, находим неизвестные члены уравнения: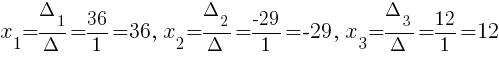
Ответ: .
Пример 10. Метод Гаусса
Дано:
Система линейных уравнений
Найти:
Решение системы линейных уравнений методом Гаусса.x1, x2, x3— ?
Решение:
Составляем расширенную матрицу (A|B) системы из коэффициентов при неизвестных и правых частей:
(A|B)=
Приведём расширенную матрицу (A|B) системы к ступенчатому виду.
Из второй строки вычитаем первую строку, умноженную на четыре:
(A|B)~
Из третьей строки вычитаем первую строку, умноженную на два:
(A|B)~
Из третьей строки вычитаем вторую строку, умноженную на :
(A|B)~
Полученной диагональной матрице соответствует эквивалентная система: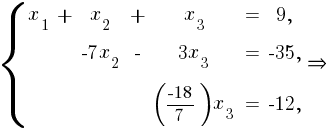
Ответ: .
Примеры решения задач онлайн с помощью WolframAlpha
1. Решение рациональных, дробно-рациональных уравнений любой степени, показательных, логарифмических, тригонометрических уравнений.Пример1. Чтобы решить уравнениеx2+ 3x- 4 = 0, нужно ввести solve x^2+3x-4=0Пример2. Чтобы решить уравнение log32x = 2, нужно ввести solve log(3, 2x)=2Пример3. Чтобы решить уравнение 25x-1= 0.2, нужно ввести solve 25^(x-1)=0.2Пример4. Чтобы решить уравнение sin x= 0.5, нужно ввести solve sin(x)=0.5
2. Решение систем уравнений.Пример. Чтобы решить систему уравнений
x+y= 5, x-y= 1,
нужно ввестиsolve x+y=5 && x-y=1Знаки && в данном случае обозначает логическое «И».
3. Решение рациональных неравенств любой степени.Пример. Чтобы решить неравенствоx2+ 3x- 4 solve x^2+3x-4
4. Решение систем рациональных неравенств.Пример.Чтобы решить систему неравенств
x2+ 3x- 4 2×2-x+ 8 > 0,
нужно ввести solve x^2+3x-4 && 2х^2- x + 8 > 0Знаки && в данном случае обозначает логическое «И».
5. Раскрытие скобок + приведение подобных в выражении.Пример. Чтобы раскрыть скобки в выражении (c+d)2(a-c) и привести подобные, нужно ввести expand (c+d)^2*(a-c).
6. Разложение выражения на множители.Пример. Чтобы разложить на множители выражение x2+ 3x- 4, нужно ввести factor x^2 + 3x — 4.
7. Вычисление суммыnпервых членов последовательности (в том числе арифметической и геометрической прогрессий).Пример. Чтобы вычислить сумму 20 первых членов последовательности, заданной формулой an = n3+n, нужно ввестиsum n^3+n, n=1..20Если нужно вычислить сумму первых 10 членов арифметической прогрессии, у которой первый членa1 = 3, разность d = 5, то можно, как вариант, ввести a1=3, d=5, sum a1 + d(n-1), n=1..10Если нужно вычислить сумму первых 7 членов геометрической прогрессии, у которой первый членb1 = 3, разность q = 5, то можно, как вариант, ввести b1=3, q=5, sum b1*q^(n-1), n=1..7
8. Нахождение производной.Пример. Чтобы найти производную функции f(x) =x2+ 3x- 4, нужно ввести derivative x^2 + 3x — 4
9. Нахождение неопределенного интеграла.Пример. Чтобы найти первообразную функцииf(x) =x2+ 3x- 4, нужно ввести integrate x^2 + 3x — 4
10. Вычислениеопределенного интеграла.Пример. Чтобы вычислить интеграл функцииf(x) =x2+ 3x- 4 на отрезке , нужно ввести integrate x^2 + 3x — 4, x=5..7
11. Вычислениепределов.Пример. Чтобы убедиться, что
введите lim (x -> 0) (sin x)/x и посмотрите ответ. Если нужно вычислить какой-то предел при x, стремящемся к бесконечности, следует вводитьx -> inf.
12. Исследование функции и построение графика.Пример. Чтобы исследовать функцию x3- 3×2и построить ее график, просто введите x^3-3x^2. Вы получите корни (точки пересечения с осью ОХ), производную, график, неопределенный интеграл, экстремумы.
13. Нахождение наибольшего и наименьшего значений функции на отрезке.Пример. Чтобы найти минимальное значение функции x3- 3×2на отрезке , нужно ввести minimize (x^3-x^2), {x, 0.5, 2}Чтобы найти максимальное значение функцииx3- 3×2на отрезке , нужно ввести maximize (x^3-x^2), {x, 0.5, 2}
Дополнительные разъяснения по работе с решателем здесь
Аналитическая геометрия
Пример 16. Уравнение плоскости, проходящей через точку перпендикулярно вектору
Написать уравнение плоскости, проходящей через точку M перпендикулярно вектору .Дано:
Координаты точек: M(2, 5, -3), M1(7, 8, -1) и M2(9, 7, 4).Найти:
Уравнение плоскости, проходящей через точку M перпендикулярно вектору .
Решение:
В качестве нормального вектора плоскости выбираем вектор = {x2-x1, y2-y1, z2-z1} = {9-7, 7-8, 4-(-1)} = {2, -1, 5}.
Уравнение плоскости, проходящей через точку M(x, y, z) перпендикулярно вектору = {A, B, C}, имеет вид 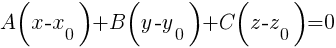 .
.
Составляем уравнение плоскости с нормальным вектором = {2, -1, 5}, проходящей через точку M(2, 5, -3):.
Ответ: .
Пример 17. Уравнение плоскости «в отрезках»
Какие отрезки отсекает на осях координат плоскость?Дано:
Уравнение плоскости: 2x – 4y + 6z – 12 = 0.Найти:
Отрезки, которые отсекает на осях координат плоскость.a, b, c — ?
Решение:
Приведем общее уравнение плоскости к виду уравнения «в отрезках»:
Уравнение — это уравнение плоскости «в отрезках». Параметры представляют собой координаты точек пересечения плоскости с координатными осями и равны (с точностью до знака) отрезкам, отсекаемым плоскостью на координатных осях.
Применяя вышеприведенное к уравнению 2x – 4y + 6z –12 = 0, получим:.
Отрезки, отсекаемые на осях, равны a = 6, b =−3, c = 2.
Отрицательный знак перед b показывает, что плоскость пересекает отрицательную полуось Oy.
Задачи по теме «Уравнение плоскости в пространстве»
Задача 1. Составить канонические уравнения прямой:
Решение:
Для составления канонического или параметрического уравнения прямой в пространстве, нужно знать координаты какой-либо точки, лежащей на этой на этой прямой, и координаты вектора, коллинеарного прямой.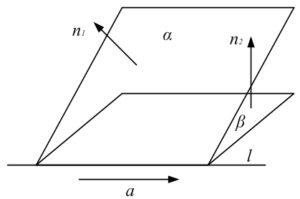
Так как прямая является линией пересечения двух плоскостей, ее направляющий вектор а параллелен каждой из этих плоскостей и соответственно перпендикулярен нормалям n1 и n2 к данным плоскостям. В таком случае он коллинеарен векторному произведению [n1, n2].n1 = (2; 1; -5), n2 = (5; 3; 8), [n1, n2] = (23; -41; 1).
Итак, (l; m; n) = (23; -41; 1).
Найдем точку, лежащую на данной прямой, у которой одна из координат принимает выбранное нами значение; тогда остальные две координаты можно определить из системы уравнений, задающей пересекающиеся плоскости.
Примем для удобства вычислений z = 0, тогда для точки A={х; у; 0}x = -4; y = 11; A = {4; 11; 0}.
Cоставим канонические уравнения данной прямой:.
Ответ: .
Задача 2. Составить уравнение плоскости, проходящей через прямую k: и точку B = {2; -3; 1}.
Решение:
Так как точка А = {-3,5,-1} принадлежит плоскости, значит вектор AB параллелен плоскости.
Так как данная прямая лежит в плоскости, ее направляющий вектор a = (2; 1; -1) параллелен плоскости.
Значит, нормаль к плоскости коллинеарна векторному произведению этих векторов.
Так как прямая лежит в плоскости, ее направляющий вектор a = (2; 1; -1) параллелен плоскости. При d = 0 из уравнений прямой получаем: — координаты точки А, принадлежащей прямой и соответственно плоскости.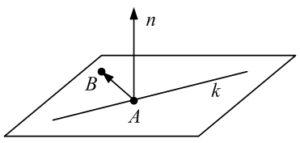
Получается, что вектор AB = (5; -8; 2) параллелен плоскости. Значит, нормаль n к плоскости коллинеарна векторному произведению = (-6; -9; -21).
Примем n = (2; 3; 7) и составим уравнение плоскости, проходящей через точку B перпендикулярно n: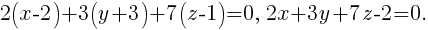
Ответ: 2x + 3y + 7z – 2 = 0.
Задача 3.Написать уравнение плоскости, которая проходит через три точки с координатами N1(x1, y1, z1), N2(x2, y2, z2), N3(x3, y3, z3).
Решение:
Предположим, что какая нибудь, находящаяся на плоскости точка N, имеет координаты (x, y, z). Для этого случая уравнение плоскости примет вид:
(r-r, a, b) = 0,
гдеr = (x, y, z);r = (x1, y1, z1);
базисные векторы (смотрите рисунок) соответственно равны и .
Если записать смешанное произведение в виде определителя, то получим необходимое уравнение плоскости:
Ответ:
Что решебник может решить
Данная программа предоставляет самую различную информацию по введенным данным. Решебник по математике англоязычный, но для решения примеров английский язык не помеха. Ниже я опишу как им пользоваться. Если хотите узнать, что он еще может — введите какое-нибудь англоязычное слово, например SUN. Уверен, он Вам понравится. Для подробного описания тех или иных правил, переходите на вкладку «Математика», там находится теоретическая часть. Для решения задач и примеров, на которые программа не знает ответа, перейдите по соответствующим ссылкам в меню. Поле решебника будет всегда в меню сверху. Удачи!